As it has been commented in the previous section, the NOE is the result of the dipolar coupling of two spins which are close in the space to each other, so that this is a distance dependent effect. However, the exact NOE dependency with distance and which NOE experiment we must carried out to obtain accurate distance measurements are not straightforward issues. Thus, for instance, steady-state NOEs cannot readily be translated into internuclear separation because they result from a balance between the influences of all neighbouring spins (only relative distances are obtained from these NOEs). It has also been shown that for molecules that exhibit negative enhancements, steady-state measurements may fail to provide any reliable information of spatial proximity, and here one is forced to consider the kinetics of the NOE. Thus, saturation of the target resonance for periods that are far less than those needed to reach the steady-state would allow some NOE to appear, which is then sampled. Repeating the experiment with progressively incremented saturation periods allows the build-up to be mapped. Owing to the use of shortened saturation periods, the enhancements observed with this method are termed truncated driven NOEs or TOEs. Although once popular, this experimental approach is rather less used nowadays and as such shall be considered no further. The more common approach to obtaining kinetic data is to instantaneously perturb a spin system not by saturation but by inverting the target resonance/s (i.e. inverting the population differences across the corresponding transitions) and then allowing the NOE to develop in the absence of further external interference. In this case, the NOE is seen initially to build for some time but ultimately fades away as spin relaxation restores the equilibrium condition; these enhancements are thus termed transient NOEs. The measurement of transient NOEs gained widespread popularity, initially in the biochemical community, in the form of the 2D NOESY experiment, which remains an extremely important structural tool in this area and increasingly in the analysis of smaller molecules. The 1D transient NOE experiment, also referred to as 1D NOESY, is also widely used within the chemical community as a gradient-selected sequence capable of providing high-quality NOE spectra. Transient experiments, whether 1D or 2D, are more commonly used qualitatively as ‘single-shot’ techniques, providing an overview of enhancements within a molecule rather than being employed to map the growth of the NOE.
Unlike the steady-state enhancements, the transient enhancements are influenced by only a single internuclear separation (r) with r–6 dependence whilst the so-called initial rate approximation is valid. Under this approach, the two cross-relaxing spins initially behave as if they were an isolated spin pair and the growth of the NOE has a linear dependence on mixing time. As longer mixing periods are used, the relaxation of spin I begins to compete with cross-relaxation between I and S, so the build-up curve deviates from linearity and the NOE eventually decays to zero (Fig. 4). Thus, for the initial rate approximation to be valid, mixing times significantly shorter than the T1 relaxation time of spin I must be used. Only under these conditions is meaningful distance measurement possible. If, on the other hand, the goal is to qualitatively identify through-space correlations, as is more often the case in routine work, mixing periods comparable to T1 provide maximum enhancements. Since transient NOEs develop in the absence of an external radio-frequency field, they tend to give rise to weaker positive values (38% maximum) than the steady-state effects (50% maximum; see Fig. 2), so careful choice of timing is crucial to the success of transient experiments with fast-tumbling molecules. With respect to the slow-tumbling molecules, owing to the domination of efficient cross-relaxation both the transient and steady-state experiments give rise to a maximum negative NOE of -100%.
The primary reason why transient NOE methodology is used, instead of the steady-state experiment, is the complications arising from the existence of spin diffusion for molecules within this regime (slow-tumbling). Thus, in this case there is also a demand for the use of short mixing periods.
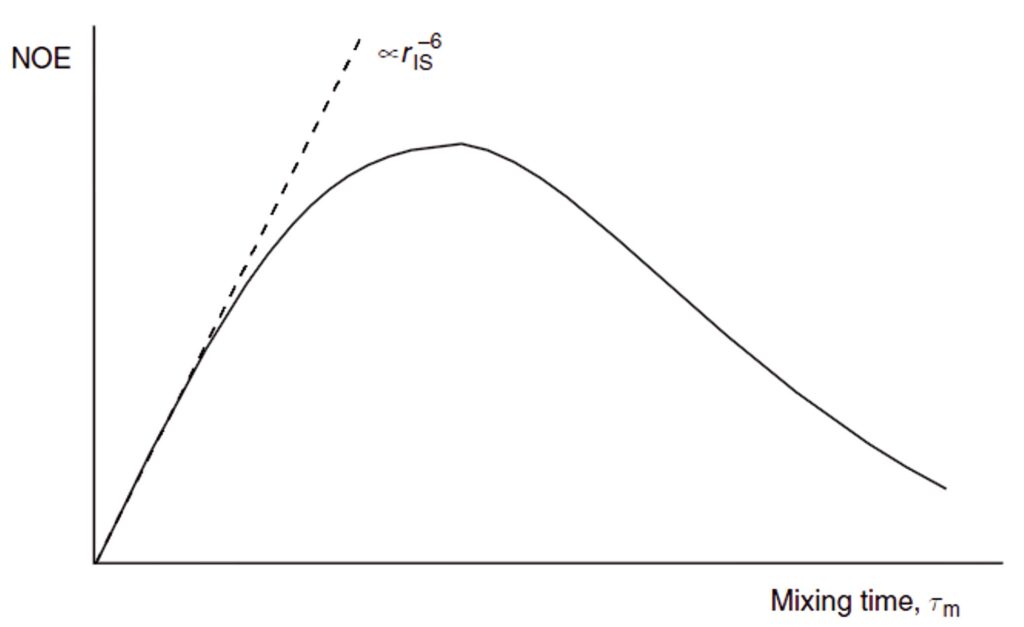
Assuming the initial rate approximation to be valid (the NOE grows linearly), the magnitude of the enhancement of spin I after inversion of spin S(niS ), after a period τm, will be proportional to the cross-relaxation rate, which in turn depends on rIS–6. Thus
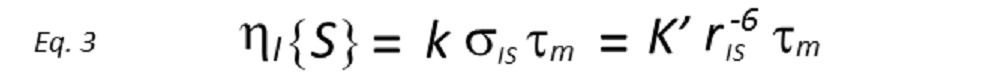
where the constants of proportionality k and k’ contain the overall correlation time of the molecule, τc, in addition to a number of known physical constants. If τc is known, rIS can be directly derived. However, whilst it is possible to determine τc from laborious relaxation time measurements, this is rarely done in practice, being more common to use a known internal distance as a reference. Therefore, if the reference NOE between nuclei A and B, of known internuclear separation rAB, is also measured, then
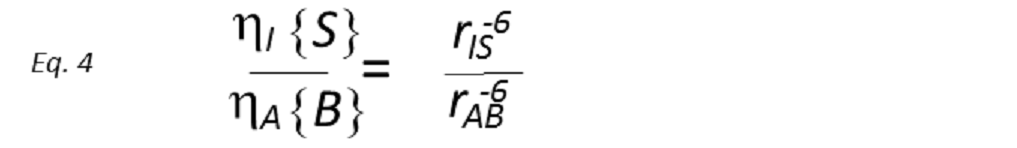
A direct comparison of the two NOE intensities thus provides the unknown internuclear distance. This simple relationship has been extensively used to provide measurements of internuclear separations, particularly in biological macromolecules. From a single experiment, distances can be estimated assuming that the initial rate approximation is valid for all interactions. This relies on all internuclear vectors in question possessing the same correlation time (i.e, isotropic tumbling), which of course is not real in all cases, e.g. when the internal motions are the main contributors to the reorientational properties of proton-proton vectors.