An accurate definition of the Nuclear Overhauser Effect (NOE) is the change in intensity of one resonance when the spin transitions of a dipolarly coupled nucleus are somehow perturbed from their equilibrium populations. This perturbation is achieved by either saturating a resonance, i.e., equalising the spin population differences across the corresponding transitions (then it is called steady-state NOE), or inverting it by reversing the population differences across the transitions (transient NOE). Thus, the magnitude of the NOE observed for spin I when spin S is perturbed (nIS) is expressed as the percentage of relative intensity change between the equilibrium intensity (I0) and that in the presence of the NOE (I), so that

The intensity changes caused by NOE can be either positive (I>I0) or negative (I0) depending on the motional properties of the molecule and the signs of the magnetogyric ratios of the spins involved.
To facilitate the understanding of the origin of the NOE, we will consider a system only formed by two homonuclear spin-1/2 nuclei of 1H (positive magnetogyric ratio), I and S, contained in a rigid molecule that tumbles isotropically in solution, i.e., it does not show any preferential axis about which to rotate. In this idealistic system both protons are not scalarly coupled (JIS=0) but they are enough close in space as to share dipolar coupling, this is, magnetic interaction through space between two spins such that both of them are able to sense the presence of the other dipolar-coupled partner. Therefore, upon selective saturation of 1H nucleus S, the spin populations of nucleus I will be also perturbed and the system will try to come back to the initial equilibrium situation. Although equilibrium recovery takes place by different relaxation mechanisms it is only the cross-relaxation pathways, characterized by the W0 (zero-quantum) and W2 (double-quantum) transition probabilities (or rates), those responsible for the NOE development (Fig. 1A). The rate at which S magnetization is transferred to I magnetization is proportional to the (W2-W0) term, known as cross-relaxation rate constant σIS.
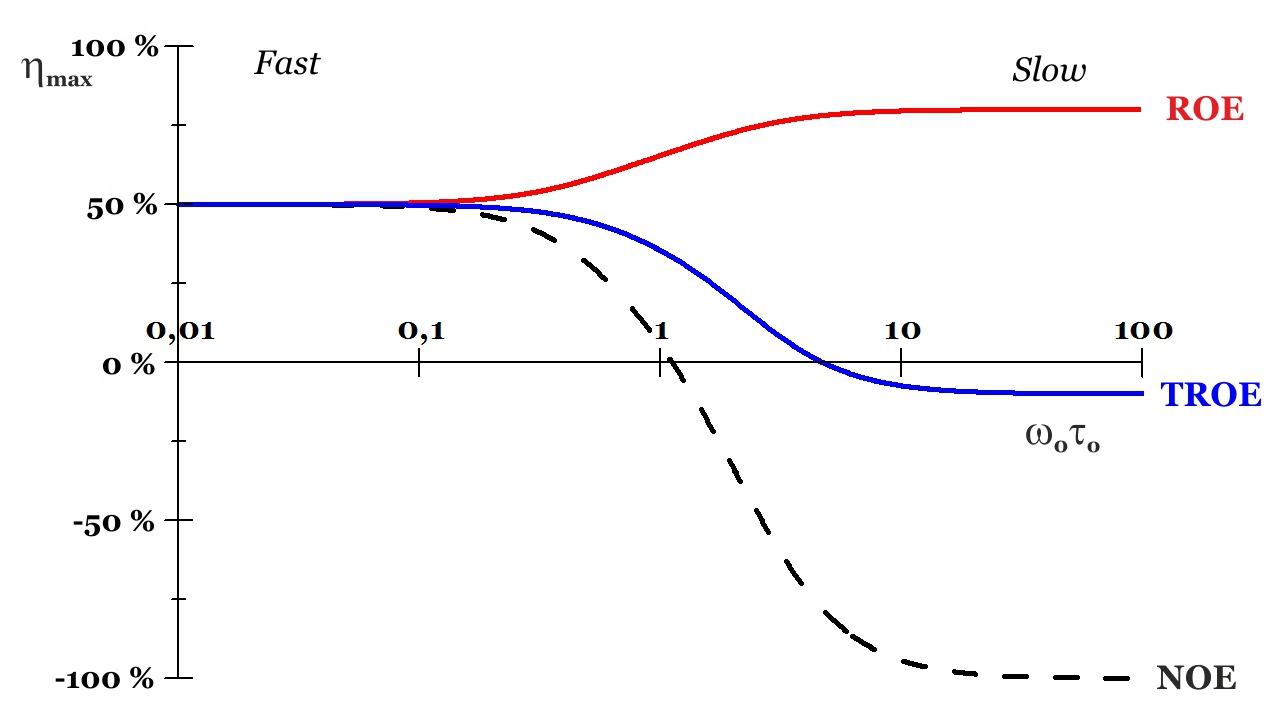
It is important to note that the W0 and W2 cross-relaxation pathways always compete with one another, with the dominant mechanism dictating the sign of the observed NOE and being dependent on the re-orientational dynamics properties of the molecule (Fig. 1B). Thus, a small molecule performing a rapid tumbling in solution, which corresponds to a short correlation time Ï„c, will generate fluctuating local magnetic fields of high frequency. On the other hand, a macromolecule, featuring slow tumbling rates (long Ï„c) will give rise to low-frequency magnetic fields. These fluctuating local fields are the responsible for inducing cross-relaxation when their oscillation frequencies correspond to the W0 and/or W2 transitions. Furthermore, those of low-frequency are significantly more efficient than the high-frequency magnetic fields in activating the cross-relaxation pathways, due to the different spectral density functions that describe the fast, intermediate and slow motions (Fig. 1B). Therefore, for slow tumbling the lower energy W0 process predominates such that a negative NOE (I0) is efficiently developed (Fig. 1B and 2). On the contrary, W2 (higher energy) is the dominant mechanism acting during cross-relaxation of fast tumbling molecules, so that a positive NOE (I0) is observed (with lower intensity compared to negative NOE; see Fig. 2). For and intermediate tumbling rate (usually medium-size molecules), the NOE will be either positive or negative depending on the dominant cross-relaxation process. Also, it has to be noted that there are two limits of motion in terms of the magnitude of the NOE developed. Thus, the rapid tumbling of a small molecule in a low viscosity solvent will favour the W2 process to a large extent, displaying high positive homonuclear NOEs. This is called extreme narrowing limit. In contrast, the slow molecular tumbling of large molecules in high viscosity solvents will stay in the spin-diffusion limit, characterised by an enormously favoured W0 mechanism, and thus, highly negative homonuclear NOEs.
Apart from the cross-relaxation mechanisms, only responsible for the NOE growth, single quantum relaxation pathways (W1) activate to re-establish the equilibrium population differences of the non-saturated nucleus (I in the simplified model) as soon as the NOE begins to develop, so acting against the NOE build-up. Thus, if W1 relaxation happens to be rather more efficient than W0 and W2 pathways together, the macroscopic magnetization will probably come back to the equilibrium before a measurable NOE is developed and this will not be observed. The NOE therefore results from the balance between distinct competing relaxation pathways, with its sign depending on the W2-W0 difference and its magnitude on the three W0, W1 and W2 rates (see Eq. 2, derived from the so-called Solomon equation).
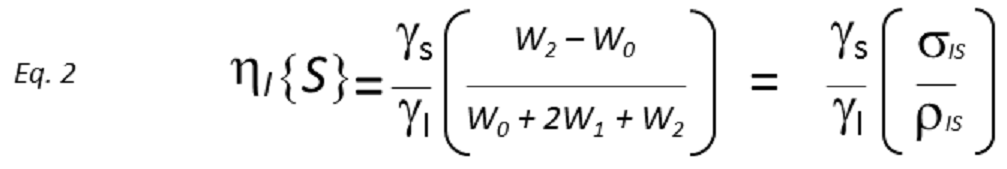
So, the ideal conditions for the NOE to be observed are inefficient W1 processes and efficient W0 or W2 transitions.