The QCM-D technique is widely used to study soft and solvated interfaces, because it enables both quantification of adsorbed mass and characterization of the viscoelastic properties of the adsorbed layer Reviakine et al., 2011. This techniques has found many applications to study fundamental biological and biotechnological questions as : adsorption of the proteins to the solid supports Muratsugu et al., 1993Caruso et al., 1997Hook et al., 2001a, proteins cross-linking Hook et al., 2001b, DNA hybridization Hool et al., 2001cLarsson et al., 2003 or DNA-drug interactions Pope et al., 2001, as well as the adhesion and spreading of cells Fredriksson et al., 1998Reiss et al., 2002. The technique is also widely used for the characterization of biofunctionalized surfacesSvedhem et al., 2003aSvedhem et al., 2003b for example, in biosensors Janshoff et al., 2000.
QCM-D is a main technique to characterize the assembly of HA-films.QCM-D afforded monitoring of adsorption processes in real time, providing detailed yet mostly qualitative information about the kinetics of layer formation, morphology and stability.
The initial screening of interactions between HA-films and the proteins used in other chapters has also typically been performed by QCM-D, although these data are not explicitly presented.
Working principle The working principle of QCM-D is based on the piezoelectric nature of quartz. The QCM-D sensor is made of a quartz crystal that is sandwiched between two electrodes and excited into a shear oscillatory movement by applying an AC electric field (Fig.1). Cutting off the external electric field results in a dampened oscillation of the crystal. By fitting an exponentially decaying oscillating curve to the data (Fig. 1D), the resonance frequency, f, of the crystal and the energy dissipation, D, are extracted. Simplistically, one could say that changes in resonance frequency, Δf, relate to the mass (including hydrodynamically coupled water) or alternatively to the thickness of the adsorbed film, whereas changes in dissipation, ΔD, relate to the mechanical (typically viscoelastic) properties of the material bound to or situated in the vicinity of the surface.
For biological applications, an important feature of QCM-D is that it operates in liquid. Work in liquid causes a response which reflects the bulk properties of the solution. The relation between the bulk properties – viscosity and density – of the liquid and the QCM-D response is following:
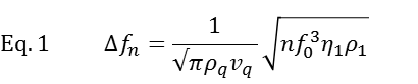
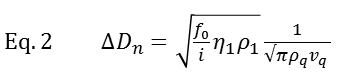
where υq is the speed of sound in quartz and by ρq – density of the quartz crystal, f0 is fundamental frequency, i is the overtone number.
Mass determination for thin and rigid, homogeneous film The adsorbed mass per surface area of the sensor crystal can be determined through the direct relation between changes in frequency, Δf, and the areal mass density, m, also known as the
Sauerbrey relation:
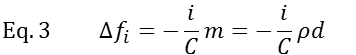
where i is the overtone number, C is the mass sensitivity constant, ρ is the density and d thickness of adsorbed film. The density of the film is often not accurately known, but fortunately, the density of most biomolecules (e.g., ρlipids ≈ 1.0 g/cm3, ρproteins ≈ 1.4 g/cm3) or polymers is rather close to that of water (ρH2O = 1.0 g/cm3), i.e. the thickness can be determined with rather good accuracy by substituting ρ with the density of water. The mass sensitivity constant C depends solely on the material properties of the sensor crystal. For a sensor with a fundamental frequency of f0 = 5 MHz, C = 18 ng/cm2/Hz).
The Sauerbrey equation is only valid for sufficiently rigid films. Sufficiently rigid films follow the oscillation of the sensor crystal with little dissipative losses. For homogeneous films, as a rule of thumb, the Sauerbrey equation can give a good approximation if the ratio ΔD/(Δf/i) is much smaller than 0.4 × 10-6 Hz-1.